Linjär utvidgning Vad är, formel och koefficienter, exempel

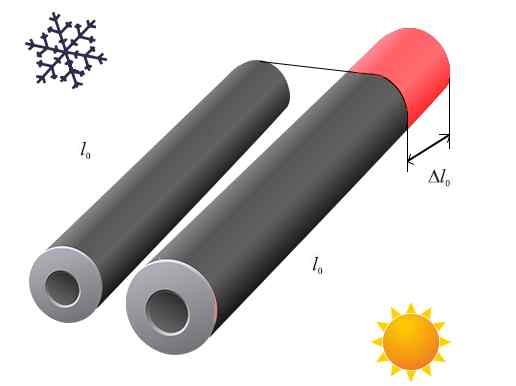
De Linjär utvidgning inträffar när ett objekt upplever dilatation på grund av en temperaturvariation, främst i en enda dimension. Detta beror på egenskaperna hos materialet eller dess geometriska form. 

Till exempel i en tråd eller i en stång, när det finns en ökning av temperaturen är den långa som lider av den största förändringen på grund av termisk utvidgning.

Fåglar poserade i ledningar. Källa: Pixabay.

Kablarna i vilka fåglarnas abborre i föregående figur har en sträcka när deras temperatur ökar; Istället drar de samman när de svalnar. På samma sätt som det händer, till exempel med staplarna som bildar rälsen på en järnväg.

[TOC]

Vad är linjär utvidgning?

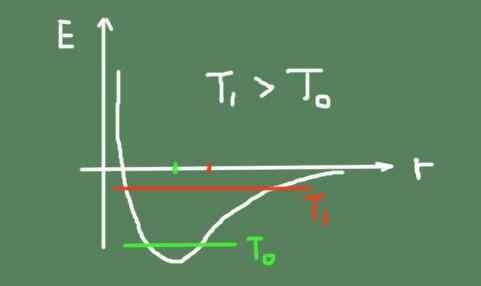Graf över energin i den kemiska bindningen kontra det interatomiska avståndet. Källa: Självgjord.

I ett fast material behåller atomer sina relativa positioner mer eller mindre fixerade runt en balanspunkt. På grund av termisk omrörning oscillerar de emellertid alltid runt den.

Genom att öka temperaturen ökar också termisk svängning, vilket gör att medelstora svängningspositioner förändras. Detta beror på att länkpotentialen inte är exakt parabolisk och har asymmetri runt det minsta.

Nedan är en siffra som beskriver den kemiska bindningsenergin beroende på det interatomiska avståndet. Den totala svängningsenergin vid två temperaturer visas också, och hur svängningscentret rör sig.

Formel för linjär dilation och dess koefficient

För att mäta den linjära utvidgningen börjar vi från en initial LE -längd och en initial temperatur T, från det objekt du vill mäta din utvidgning.

Anta att detta objekt är en stapel vars längd är L och dimensionerna på tvärsnittet är mycket lägre än L.

Kan tjäna dig: omedelbar acceleration: vad är det, hur det beräknas och övningar

Först underkastas detta objekt en ΔT -temperaturvariation, så att objektets slutliga temperatur när värmejämvikten har fastställts med värmekällan kommer att vara t '= T+ ΔT.

Under denna process kommer objektets längd också att ha ändrats till ett nytt värde L '= L + ΔL, där ΔL är variationen i längd.

Den linjära dilationskoefficienten a definieras som förhållandet mellan den relativa variationen av längd per temperaturvariation. Följande formel definierar den linjära dilationskoefficienten a:

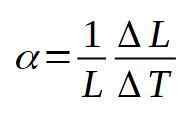I de flesta fallen, a Den har ett konstant värde för temperaturer mellan (t - ΔT) och (t + ΔT).

Måtten på den linjära dilationskoefficienten är temperaturen.

Temperaturen ökar längden på rörformade fasta ämnen. Detta är vad som kallas linjär utvidgning. Källa: Lafer.com

Linjär dilationskoefficient för olika material

Därefter ger vi en lista över den linjära dilationskoefficienten för vissa typiska material och element. Koefficienten beräknas i normalt atmosfärstryck baserat på en omgivningstemperatur på 25 ° C; och dess värde betraktas konstant i ett intervall av upp till 100 ° C.

Den linjära dilationskoefficientenheten kommer att vara (° C)^-1.

- Stål: α = 12 ∙ 10^-6 (° C)^-1

- Aluminium: α = 23 ∙ 10^-6 (° C)^-1

- Guld: α = 14 ∙ 10^-6 (° C)^-1

- Koppar: α = 17 ∙ 10^-6 (° C)^-1

- Mässing: α = 18 ∙ 10^-6 (° C)^-1

- Järn: α = 12 ∙ 10^-6 (° C)^-1

- Glas: α = (7 till 9) ∙ 10^-6 (° C)^-1

- Kvicksilver: α = 60,4 ∙ 10^-6 (° C)^-1

- Kvarts: α = 0,4 ∙ 10^-6 (° C)^-1

- Diamant: α = 1,2 ∙ 10^-6 (° C)^-1

- Bly: α = 30 ∙ 10^-6 (° C)^-1

Det kan tjäna dig: konvektionsvärmeöverföring (med exempel)

- Ekved: α = 54 ∙ 10^-6 (° C)^-1

- PVC: α = 52 ∙ 10^-6 (° C)^-1

- Kolfiber: α = -0.8 ∙ 10^-6 (° C)^-1

- Betong: α = (8 till 12) ∙ 10^-6 (° C)^-1

De flesta material sträcker sig med en temperaturökning. Vissa specialmaterial som kolfiber krymper med temperaturökningen.

Löst exempel på linjär expansion

Exempel 1

En kopparkabel hängs mellan två stolpar, och dess längd på en sval dag vid 20 ° C är 12 m. Beräkna värdet på dess längd på en varm dag vid 35 ° C.

Lösning

Från definitionen av den linjära dilationskoefficienten och att veta att för koppar är denna koefficient värt: α = 17 ∙ 10^-6 (° C)^-1

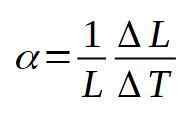
Ökningen i längd ges av: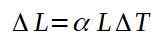

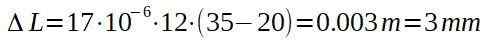
Kopparkabeln genomgår en ökning i sin längd, men detta är bara 3 mm. Det vill säga kabeln går från att ha 12 000 m till att ha 12,003 m.

Exempel 2

I en smed lämnar en aluminiumstång ugnen vid 800 grader Celsius och mäter en längd på 10,00 m. När den svalnar till den omgivningstemperaturen på 18 grader Celsius, bestäm längden som stången kommer att ha.

Lösning

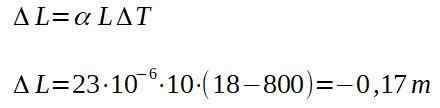
Det vill säga att baren, en gång kall, kommer att ha en total längd på:

9,83 m.

Exempel 3

En stålnit har en diameter på 0.915 cm. Ett 0,910 cm hål görs på en aluminiumplatta. Detta är de initiala diametrarna när omgivningstemperaturen är 18 ° C.

Vid vilken minsta temperatur ska plattan värmas så att niten passerar genom hålet? Syftet med detta är att när järnet återgår till rumstemperaturen justeras niten på plattan.

Kan tjäna dig: Parallelogram Metod: Exempel, lösta övningar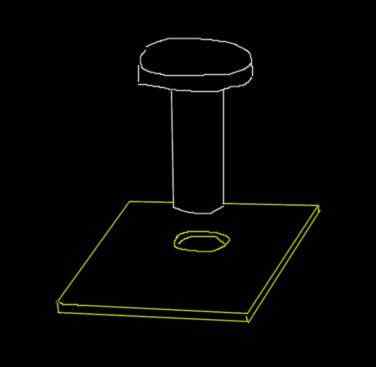Figur till exempel 3. Källa: Självgjord.

Lösning

Även om plattan är ett område är vi intresserade av utvidgning av håldiametern, som är en en -dimensionell mängd.

Låt oss ringa D₀ till den ursprungliga diametern på aluminiumplattan och D som en gång kommer att uppvärmas.

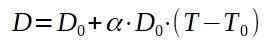
Rensa den slutliga temperaturen t, du har:

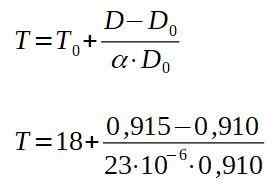
Resultatet av de tidigare operationerna är 257 ° C, vilket är den minsta temperaturen vid vilken plattan måste värmas upp så att niten passerar genom hålet.

Exempel 4

Niten och placken i den tidigare övningen placeras tillsammans i en ugn. Bestäm vid vilken minsta temperatur ugnen måste vara så att stålniten passerar genom aluminiumplatthålet.

Lösning

I detta fall kommer både niten och hålet att försena. Men stålutvidgningskoefficienten är α = 12 ∙ 10^-6 (° C)^-1, Medan aluminiumet är α = 23 ∙ 10^-6 (° C)^-1 .

Vi letar sedan efter en slutlig temperatur t så att båda diametrarna sammanfaller.

Om vi ​​ringer 1 till niten och 2 till aluminiumplattan letar vi efter en slutlig temperatur t så att D₁ = D₂.

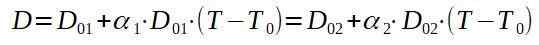
Om vi ​​rensar den slutliga temperaturen T har vi:

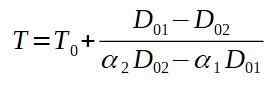
Därefter placerar vi motsvarande värden.

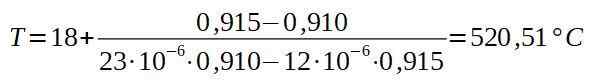
Slutsatsen är att ugnen måste vara minst 520,5 ° C så att niten passerar genom aluminiumplatthålet.

Referenser

1. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte upplagan. Prentice hall. 238-249.
2. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. Mac Graw Hill. 422-527.