Formel och ekvationer spänning, beräkning, övningar

han Stressstam Det definieras som kraften vinkelrätt mot området per enhetsområde som appliceras på ett föremål i dess ändar för att utöva dragkraft på den, tack vare vilken den förlänger. Dess dimensioner är av kraft / område och i matematisk form kan vi uttrycka det enligt följande:

τ = f / a

Enheten i ansträngningen i det internationella enhetssystemet är densamma som används för tryck: Pascal, förkortad PA, vilket motsvarar 1 Newton/ m².

Figur 1. Om spänningsinsatsen överstiger ett visst värde bryts repet. Källa: Pxhere.

I spänningsinsatsen finns det två krafter som gäller i samma riktning och motsatta sinnen, som sträcker kroppen. Om objektets längd ursprungligen var l_antingen, Vid tillämpning av spänningsinsatsen är den nya längden L och ΔL -sträckningen beräknas av:

Δl = l - l_antingen

Fasta föremål har elasticitet i större eller mindre utsträckning, vilket innebär att när spänningsinsatsen försvinner återgår de till sina ursprungliga dimensioner.

Detta händer förutsatt att ansträngningen inte är så stor att det orsakar permanent deformation. Gummi, gummi eller gummimaterial är bra för elastiska föremål och har också detta kvalitetshår och hud, bland andra.

[TOC]

Enhetlig deformation

När du studerar hur kroppar deformeras under spänning är det mycket bekvämt att definiera begreppet Enhetlig deformation, En släppt kvantitet. Enhet deformation betecknas med den grekiska bokstaven Δ (små bokstäver "delta") och beräknas enligt följande:

Δ = Δl /l_antingen

Enhet deformation tjänar till att relativt bedöma deformation av objektet under spänning. Låt oss se det på detta sätt: det är inte detsamma att sträcka 1 cm en stång på 1 meter lång, för att sträcka 1 cm till ytterligare 10 m lång. I det första fallet är deformation mycket mer betydande än i den andra.

Det kan tjäna dig: ohm: motståndsmått, exempel och träning löst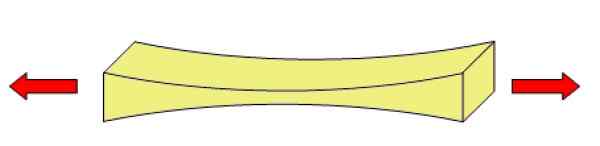figur 2. Ett objekt som genomgår en spänning eller dragkraft deformeras. Källa: Wikimedia Commons.

Hur beräknas spänningsinsatsen? (Exempel)

Newtons engelska och samtida fysiker vid namn Robert Hooke (1635-1703), undersökte kroppens elastiska egenskaper och etablerade lagen som bär hans namn. Med det är den ansträngning som tillämpas på deformation som upplevs när ansträngningen är liten relaterad:

Ansträngning ∝ Deformation (Unital)

Det är logiskt att förvänta sig att ju större stressinsats, större förlängning kommer att inträffa. Använd de definitioner som anges ovan:

τ ∝ Δ

Proportionalitetskonstanten som är nödvändig för att fastställa jämlikhet betecknas och är känd som den unga modulen eller elasticitetsmodulen, karakteristisk för materialen:

τ = y⋅δ

Youngs modul har samma enheter av spänningsinsats, eftersom enhetsdeformationen är dimensionlös.

Så ett sätt att beräkna stressansträngningen i en kropp med elastiska egenskaper, mäter deformation och känner till dess unga modul. Detta belopp har fastställts experimentellt för många material och tabelleras.

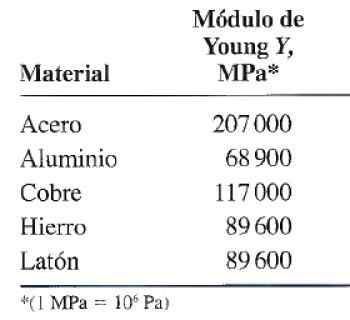Figur 3. Youngs elasticitets- eller modulmodultabell för vissa vanliga användningsmaterial. Källa: Valera Negrete, J. 2005. Allmänna fysikanteckningar. Unk.

Exemplet på beräkning

Anta att en 3 mm diameter härdad stål utsätts för en spänningsinsats, hängande från det en vikt på 250 n, vad skulle vara storleken på nämnda ansträngning?

Vi kan använda definitionen av spänningsinsats som kvoten mellan kraften vinkelrätt mot ytan och området på nämnda ytan. Låt oss beräkna området först, förutsatt att en cirkulär tvärsektionstråd:

Det kan tjäna dig: Massnummer: Vad är det och hur man får det (med exempel)

A = π . (D/2)² =  π . (D² /4)

Trådens diameter är 3 mm och dessa enheter måste omvandlas till mätare:

D = 3 x 10^-3 m.

A = π . (3 x 10^-3 m)² / 4 = 7.07 x 10^-6 m².

Spänningsinsatsen produceras av vikten som hänger från tråden, som appliceras vinkelrätt mot dess tvärsnitt, därför:

τ = 250 n / 7.07 x 10^-6 m² = 3.5 x 10 ⁷ Pa

Pascal är en ganska liten enhet, så multiplarna är inte ovanliga. Att veta att 1 mega-pascal (MPA) är 10⁶ Pascal, spänningsinsatsen kvarstår:

τ = 35 MPa

Löst övningar

- Övning 1

Elasticitetsmodulen för en stång är 4 x 10^elva Pa. Vilken enhetsdeformation erhålls genom att tillämpa en spänningsinsats på 420 MPa?

Lösning

Ekvationen som ska användas är:

τ = y⋅δ

Med det beräknar vi den enhetliga deformationen:

Δ = τ / y = 420 x 10⁶ PA/ 4 x 10^elva Pa = 0.00105

Δ = Δl /l_antingen

Därför är deformationen ΔL:

ΔL = 0.00105 L_antingen

Om till exempel stången var ursprungligen 1 meter lång, med den spänningsinsatsen sträcker den bara 0.00105 m = 1.05 mm.

- Övning 2

En ståltråd har 1.50 m lång och en diameter på 0.400 mm. En av ändarna är fäst vid taket och en massreflektor placeras på den andra m = 1.50 kg, som släpps. Beräkna:

a) trådsträcka.

b) enhetlig deformation och enhetlig deformationsprocent. Är det möjligt att tråden bryts av reflektorns vikt?

Lösning

Tråden kommer att sträcka sig, eftersom reflektorn utsätts för en spänningsinsats. Kraften som produceras av denna ansträngning är reflektorens vikt.

Det kan tjäna dig: fysik före grekerna (Antigua Grekland)

Vikten på ett massobjekt är produkten av massan genom värdet på tyngdkraften, därför:

F = 1.50 kg x 9.8 m/s² = 14.7 n

Tvärsnittet av trådsektionen behövs:

A =  π . (D² /4) = π x (0.4 x 10-3 m) 2 /4 = 1.26 x 10^-7 m².

Med dessa resultat beräknas ansträngningen på tråden:

τ = 14.7 n / 1.26 x 10^-7 m² = 1.17 x 10⁸ Pa

Tråden har ett elastiskt beteende, därför är det giltigt att anta att Hookes lag är uppfylld:

τ = y⋅δ

Från tabellen Elasticitetsmodul finner vi att för stål y = 207 x 10⁹ Pa. Dessutom är enhetlig deformation:

Δ = Δl /l_antingen

Ersätta i ekvationen för ansträngningen:

τ = y⋅Δ = y⋅ (Δl /l_antingen)

Därför är sträckningen:

Δl = l_antingen τ / y =

= 1.50 m x 1.17 x 10⁸ PA / 207 x 10⁹ PA = 8.5 x 10^-4 m = 0.849 mm.

Den enhetliga deformationen av tråden är:

Δ = Δl /l_antingen = 8.5 x 10^-4 m / 1.5 m = 5.652 x 10^-4

Om vi ​​uttrycker det som en procentandel är den procentuella enhetsdeformationen 0.0565 %, mindre än 0.1 %, därför förväntas det att tråden motstår reflektorvikten utan att bryta, eftersom deformation som den upplever inte är för stor jämfört med den ursprungliga längden.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Öl, f. 2010. Materialmekanik. McGraw Hill. Femte. Utgåva.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.
5. Valera Negrete, J. 2005. Allmänna fysikanteckningar. Unk.